賭徒遊戲
假定你是一個賭場的賭客很幸運的找到了一個公平的賭博遊戲──在每一次賭局中你和莊家都各有50﹪的勝面。這或許是輪盤賭具,沒有平手的機會。你賭紅色或黑色,每一色出現機率完全相同。你口袋有十塊錢進場,而以一塊前壓紅色出現。假使輪盤出現吃紅色,你贏一塊前,在你有了十一塊錢賭資。如果出現黑色,你輸了一塊錢,因而僅剩下九塊錢。繼續下去,賭本會在一塊錢的範圍內擺動,直到下面三種情況之一出現為止:(1)你破產了,(2)賭場破產了,(3)你用盡了時間或者另外理由決定離開。
圖3-1顯示在賭場戲碼的幾種可能狀況。雖然利用家裡個人電腦模擬的隨機數字遊戲,它們可能輕易的用翻轉硬幣方式或者利用紅與黑花色的紙牌來進行遊戲。在每一種模式中我們的賭客最後都面臨著破產,但是在模式3中,賭客確實有一陣子狀況極佳。
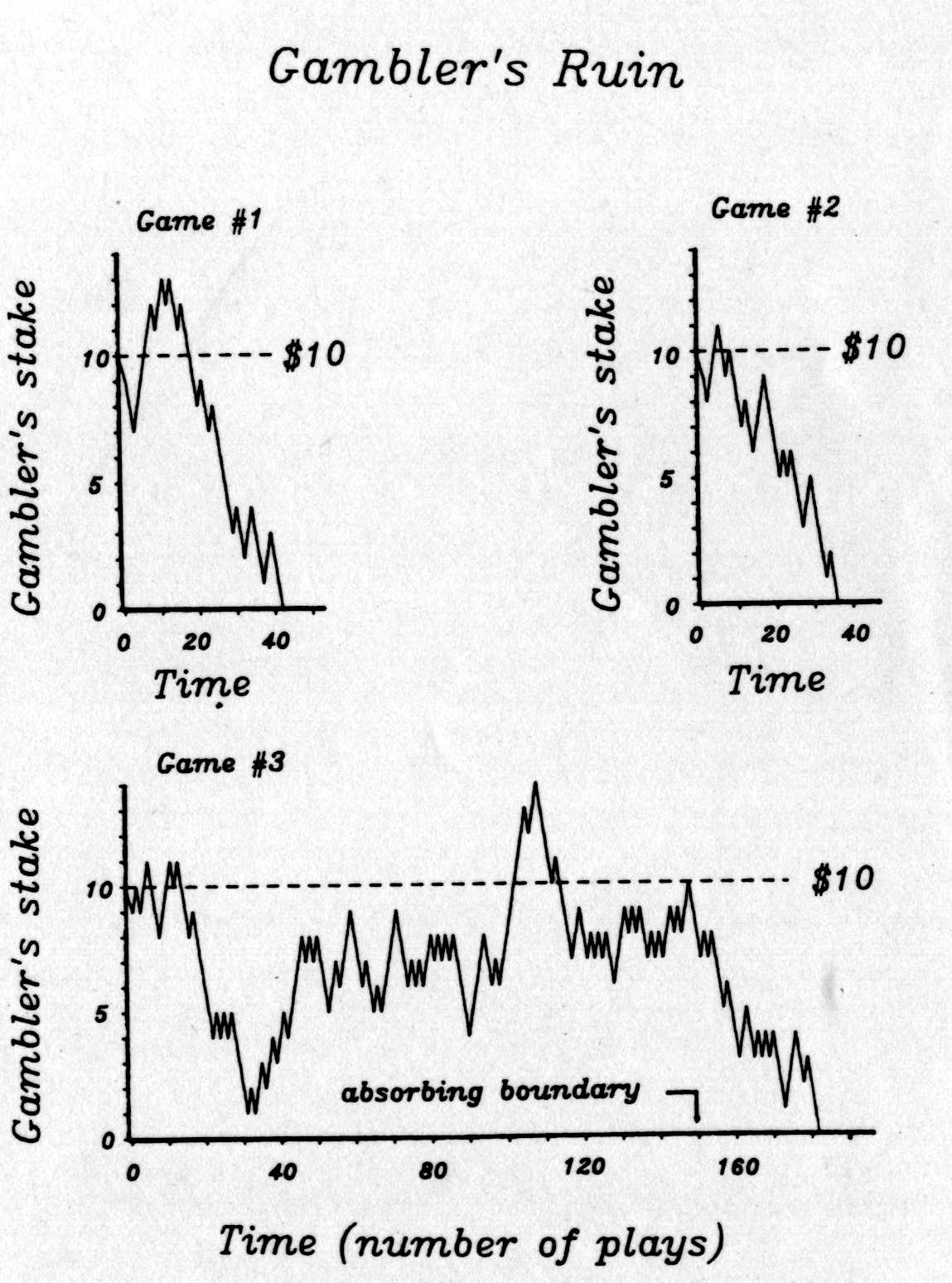
<圖說3-1:在機會均等賭局(即賭客確實與莊家各擁有每一局50﹪的勝面)中,模擬的賭博結局。賭客最初始的賭資為十元,每一次下注一元。因此賭資隨機的波動上或下的範圍內。賭客結束賭局當達到引人入勝的臨界點─零點─到達時。每一個遊戲就像是一個生物屬具有開始時10個生物種的存在的命運。當種分岐產生另一新種時,生物種的數字上昇,而當生物種滅絕時,則轉趨下降。>
剛剛討論到的最簡單形式的賭客破產問題,被統計學者引用好幾年做為一種機率的模式。無可避免的,關於賭徒破產,有好多特殊專有名詞來描述。比方說,沿著圖3-1之中賭徒運氣的路徑稱之於〝隨機行走(random walk)〞。一旦開始,隨機行走就不會傾向於回到原來所占有的層次位置。假始賭客開始於十元的賭資,沒有任何力量驅使這個路徑保持接近十或者重回到十的位置。這個系統不具有記億性。當然即令最好的賭客也知道這件事:冗長失敗之途並不會改變勝算而致富。
在圖3-1中每一圖的水平基面代表了零賭資──即賭徒失掉原來所有的賭資而面臨破產之境。這個基面稱為─〝吸取界限(absorbing boundary)〞,因為如果路徑達到這個層次,無回頭路,遊戲即刻終止。我們能夠改變這個條件,假定當你破產時,賭場給你一塊錢繼續玩遊戲。在這情況下,圖的下方變成為一個反轉界限(reflecting boundary)──你至少可以有往上一步的反身機會。我不知道有任何賭場會幹這種事,除非你事先提出了戶頭。
在圖3-1中的第三個遊戲,賭客在遊戲中很早就從10塊賭資落到1塊錢的谷底,然後昇到14塊,而最終落到零的吸收界限。假設賭客開始時賭資為九塊錢而不是十塊錢,而遊戲其它部份類似。那麼零點將出現在開始的滑落趨勢上,賭客就絕不會享有爾後短暫成功的樂趣──以及離開享有小小的樂趣。這就強調了最開始賭資大小的重要性:開始越高,那麼離吸收界限就越遠,就越可能賭客保持玩遊戲的時間就越長。
理論上,賭場能夠藉著提供一個機會均等而實質獲益,祇要它們規定賭客每次下注的上限即可。這是因為典型的賭客進到賭場所擁有的賭資較莊家遠遠接近於零點的界限。在賭徒破產問題中其上界也是個吸收界限(賭徒破產),但是這個界限通常太高,對每一個別的賭客而言不太關切亦無關聯。然而,考量到一個豪客進到公平賭局,具莊家剛好一半的原始賭本。假如這個賭客被允許玩的足夠久或者下注足夠大,那麼他讓莊家破產的機會是50﹪。
在滅絕的議題中,我們或許想像賭客的資本就相當於在演化族群中的生物種數量。我們原始賭資十元的例子或許是一個屬中10個種生存的在地史上某一時段裡。我們將使用地質時間尺度的百萬年單位,而不是賭局的時間尺度。在每一個百萬年的時距中,每一個種存活到下一個百萬年的機運是50﹪。假如它存活了。它就有50﹪機會產生新種。那麼對這個屬的命運我們能夠做什麼樣的預測呢?
幾個有趣的預測是可能的。例如,〝生物種的數量(即生物多樣性)就會像在隨機行走模式中一樣上下波動〞。生物滅絕降低了多樣性;生物種化形成新種則增加多樣性。祇要滅絕和產生新種的機會相同,則產生了隨機遊走的結果。
更進一步,〝最終屬的滅絕是無可避免的〞。這是有些反直覺的,但它卻依循著一個在〝零點種〞的吸收界限存在的事實。我們已經看到,隨機遊走是自由的上下波動,無限制的。如果沒有上限,那麼隨機遊走最終會趨使達到其下限。
當然我們能夠特定出一個上限,相類比於賭場的所有資產。在全球生物的內涵中,其中吸收界限或許將會〝銀行導致破產〞經由產生新種過量,而使得其它的屬無從存在。那麼全球所有的種都將屬於同一個屬了。這就像正常賭客贏了整個賭場一樣不太可能的。因而,在所有實際的目的下,一個屬最終的滅絕是可預期到的。
隨機選取的概念
在自然界中,隨機選取的意義為何?擲幣猜正反面被稱為隨機的。對大多數人而言,其結果就純然是機運的問題──沒有任何原因的。但是錢幣的投擲肯定是受制於因果的。幣的正面或反面朝上,依賴於幾乎是無法估算的物理因素,包括了開始擲之前的朝上的方向,投擲力道──因而牽涉到錢幣在空中翻轉的次數。同時重要的也在於氣流的狀態(包含風的因素)同時或許包括了大氣壓力,我們還未論到錢幣自身的狀態。(幾乎同樣的狀況是馬蹄鐵的投擲,順便一提,好的玩家甚而能夠控制馬蹄鐵在空中轉的次數呢!)。錢幣的投擲是如此複雜以致我們無法或選擇不去模擬所有決定的因子。
換個方式,我們選擇去假設這種複雜的原因將合成使得錢幣投擲起來像是其作用為隨機的。既選擇了這樣的前提下,我們就可以忽略掉所有氣流及其它的細節,同時歸諸於統計學上的假想正面與反面是機率相同的。這緊接著,可以執行數學的作業來涉及隨機的事件,能夠讓我們去回答一些問題,諸如:在一連續反面出現二十次的的機率有多大?假想為隨機是一個伴隨的複雜性,我們能夠有一個可依循的現象以致我們得以獲致有趣並有用的預測。
大部份的科學家與哲學家現在都同意,在自然界沒有什麼事物是真正隨機的。氣體中分子的移動,冰川的前進,颱風的形成,地震的形成,以及傳染病的散佈都有其緣由。在某些例子中是可能同時值得去查其緣由的。尤其在地震與疾病中確實如此。但在一些其它模式中,我們無法或選擇不去了解去認知。比方說。假設在氣體中分子的移動為隨機的。我們能夠得到氣體定律(Boyle’s定律等),那對於無數工程上的應用至關重要。
或許在自然體系中對隨機最佳定義是:〝所謂隨機事件就是指那些事件除去其或然率外,無可預測的〞。大約70﹪的降雨預測就是這樣的範例。
應用賭徒破產的方法至滅絕概念上,我們談論到類似的可能性。我們假設有許多原因,或許因素很大,使得生物走向滅絕之途。我們觀察在化石紀錄中滅絕的模式幾不可分。談論到生物種的命運,這相當是說假如一個壓力或者災難沒有碰到你頭上,另外一個必然還會一樣。一旦我們假設了這種隨機的行為之後,我們就可以隨心所欲的來操作這個模式。這樣的門徑得以建構可能的普遍性歸納,那是較陳襲舊式個案研究所無法達成的。
為生存而豪賭
在一個屬或者任何相關聯種的族群其演化史中,都存在剛剛所討論到的某些隨機的概念。非常複雜的物理及生物因子將會決定一個屬中每一個種將會存活多長以及種是否會分支形成新的種。種的滅絕使該屬的前景減弱,而種的形成則保護其存活。曾經有人認為,屬並非為生存而奮鬥──它們事實上是在豪賭。
僅藉由好運道本身。一個屬(或任何其它的族群)或許能生存一段時間,就如同一個賭徒或許能以戲劇性的成功。更進一步而言,假使經由好運道而產生許多的生物種──相當於在賭場裡大贏家一樣──使得該屬在未來幾百萬年內滅絕的機會將大為降低。因而大量的生物種存在將提供給這個族群暫時保護不致於滅絕掉。
今天在現生的哺乳動物中存在有較多的囓齒目(大約一千七百多種)。其次在分歧度上較多的是蝙蝠類,大約多於900種。因而,幾乎所有現生哺乳動物之種三分之二是囓齒類或者蝙蝠類。這可能僅因為是運氣好嗎?這族群有可能是在生存史中早期享有新種產生之樂,或者幸運的免於滅絕之命運?或者它們祇是緣於某種特定的生物原因而在存活以及/或是新種產生方面特別專長?
在決定這兩者之間的可能性時,一個困惑在於隨機的作用機制具有非常廣泛的產出物;在那個寬廣範圍間,其格位通常是不可預測的。對囓齒類或者蝙蝠的問題在於:這個族群的演化史是否在一個勝負均等賭局所期望極限之內,或者新種產生的過剩已經超出合理的統計學上的期望?假若後者是正確的,那麼它們必然做了什麼正確的事情。在Will Cuppy所撰寫〝如何造成滅絕〞一書中,他認為知道這個答案。他寫道〝蝙蝠也將噗通墜地,每一個人都知道,除了蝙蝠它們自己茫然未覺〞。
不同的滅絕與新種發生的效率
在所有這些討論中,我一直假設新種的發生與滅絕的速率是相同的。就好像一個種的誕生與的死亡被認定純然相同一樣。這種情況怎麼可能成為事實?尤其是種的誕生與種的死亡是如此不同的現象。
有兩種回答方式。首先隨機游走的邏輯引申極適切,具有不相等的機率──僅需將其數學程式稍為修改即可。回到賭場的戲碼,莊家正常情況下建構一個機率上的不平衡,因而獲利較大。這時隨機游走仍然可以適用但是偏頗稍為對顧客不利而已。因此,我們可以輕易的操作像演化的模式,其中新種產生與滅絕可能是不同的。比方說,我們能期望,囓齒類與蝙蝠曾經生存在其新種的產生較滅絕更普遍。我們前面提到過,囓齒和蝙蝠僅是太幸運了能贏得均等遊戲中的勝局。有些賭徒確實贏錢而且還是經常性的勝利者。
關於假設速率相等的第二個對這個問題的答覆是注意到在生命歷程中所有新種發生事件的總數和所有滅絕與存活現生種比率為1000:1。假若在地史中有四百億的生種曾經存在過,同時假定今天有四千萬的現生種(要記在心裡我們並不知道確實的數目),那麼必然曾經有四百億的新種發生,同時有三百九十九億九千萬的種曾經滅絕。因此,從長期平均的新種產生率和滅絕率大致是相同的。不論這種相近速率的原因如何,這些數字顯示一個輸贏均等模式是合理的。
不對稱的柱狀分布圖
古生物學者曾經做了許多的電腦模擬以便獲取一些關於在生物多樣性隨機游走結果的範圍概念,假設同樣或者相異的種發生與滅絕速率的不同情況。有些模擬的族群能夠擴張到超出了電腦的容量;而另有一些結果很快到達了滅絕境地。當最初始的族群很小時,族群的滅絕最為普遍,就好像在賭場的賭客如果一開始時賭資很小,接進於吸盡臨界線,最可能很快的就會破產。
在演化中,根據定義一個群體比方是屬或者科必然始於單一種。對初生的族群要存活,這個奠基的生物種必然要在滅絕之前,形成新種。因為新的演化族群,開始時很小,通常他們無法持續很長的時間。這個因而在生命歷程中產生一個很重要的局面:大部分生物種的族群,其生命的歷程較之所有族群平均值為短。圖3-2顯示化石屬其生命時程的柱狀分佈。具有一不對稱的歪形,非常多的短暫時程而僅有少數的長期生命時程。
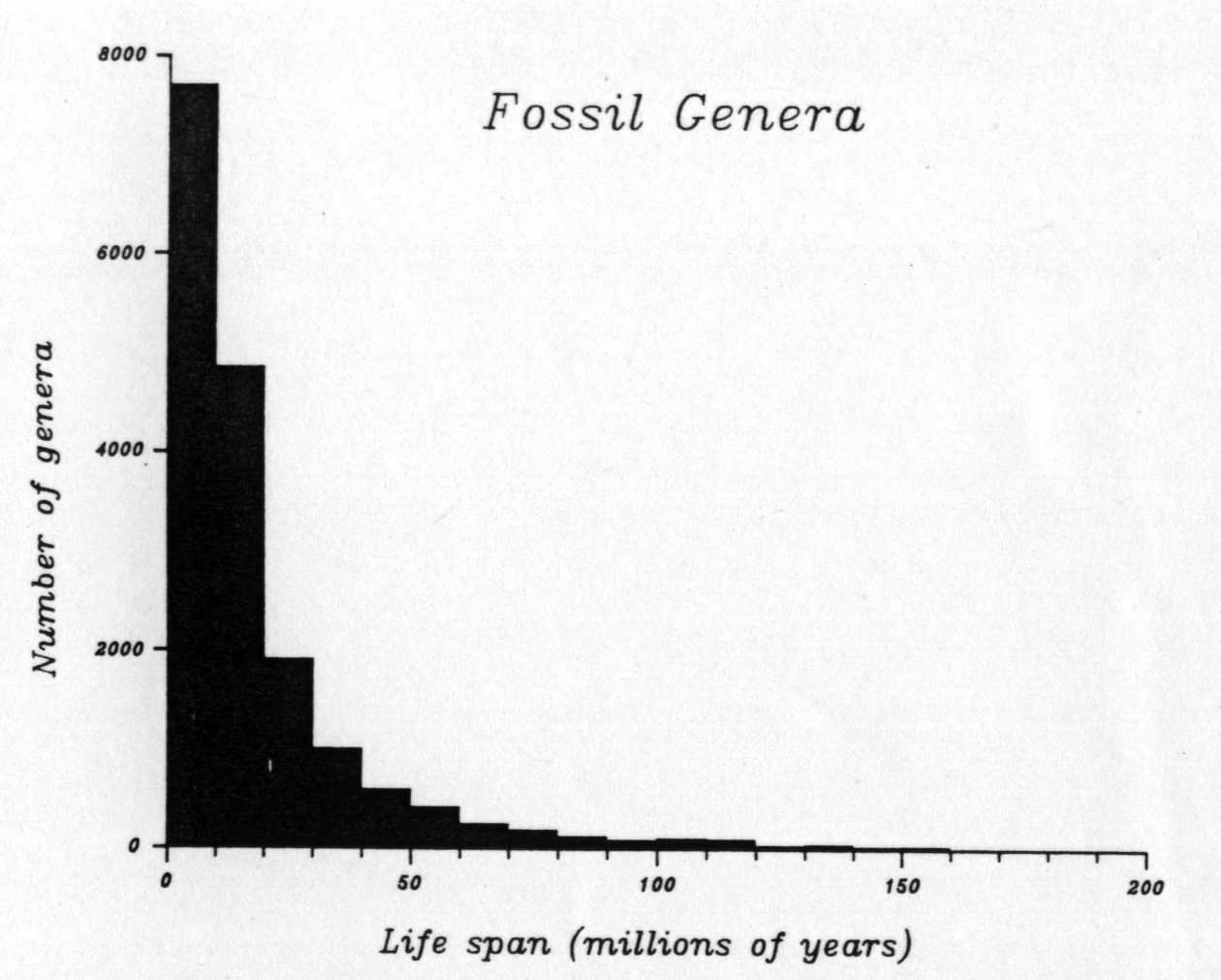
<圖3-2解說:柱狀圖中顯示在化石屬中地質生命時程的分佈狀況。在化石屬其平均存活時程大約二千萬年。這個圖呈高度不對稱的歪形──與長於平均值的生物總數相比,有遠遠多量的生物種其存活時程低於平均值。(根據J.J. Sepkoski所統計17,505個生物屬的從活時程資料而來)。>
這種不對稱的歪形變異在與滅絕問題密切相關的重要生物特性中是極特別的。這包括了:(1)在一個屬中種的數量,(2)生物種的生命時程,(3)一個生物種中的個體數量,以及(4)種的地理分佈。
在每個項目中,較小的〝事物〞是最為普遍的。讓我提另一個例子。現今生存大約有4000種哺乳動物,形成大約1000個屬。大約有一半的屬僅有單一種,約15﹪有兩個種。這個數字如圖3-3所示很緩慢的下滑,因此,僅有少數的屬具有超過25個生物種。再現生哺乳動物屬中最繁盛的大約有160個種(小型食昆蟲動物)。平均每一個屬大約有四個種(4,000/1,000),但是因為其不對稱性的歪形,全部四分之三的屬具有1,2或3個生物種,因而低於其平均值。
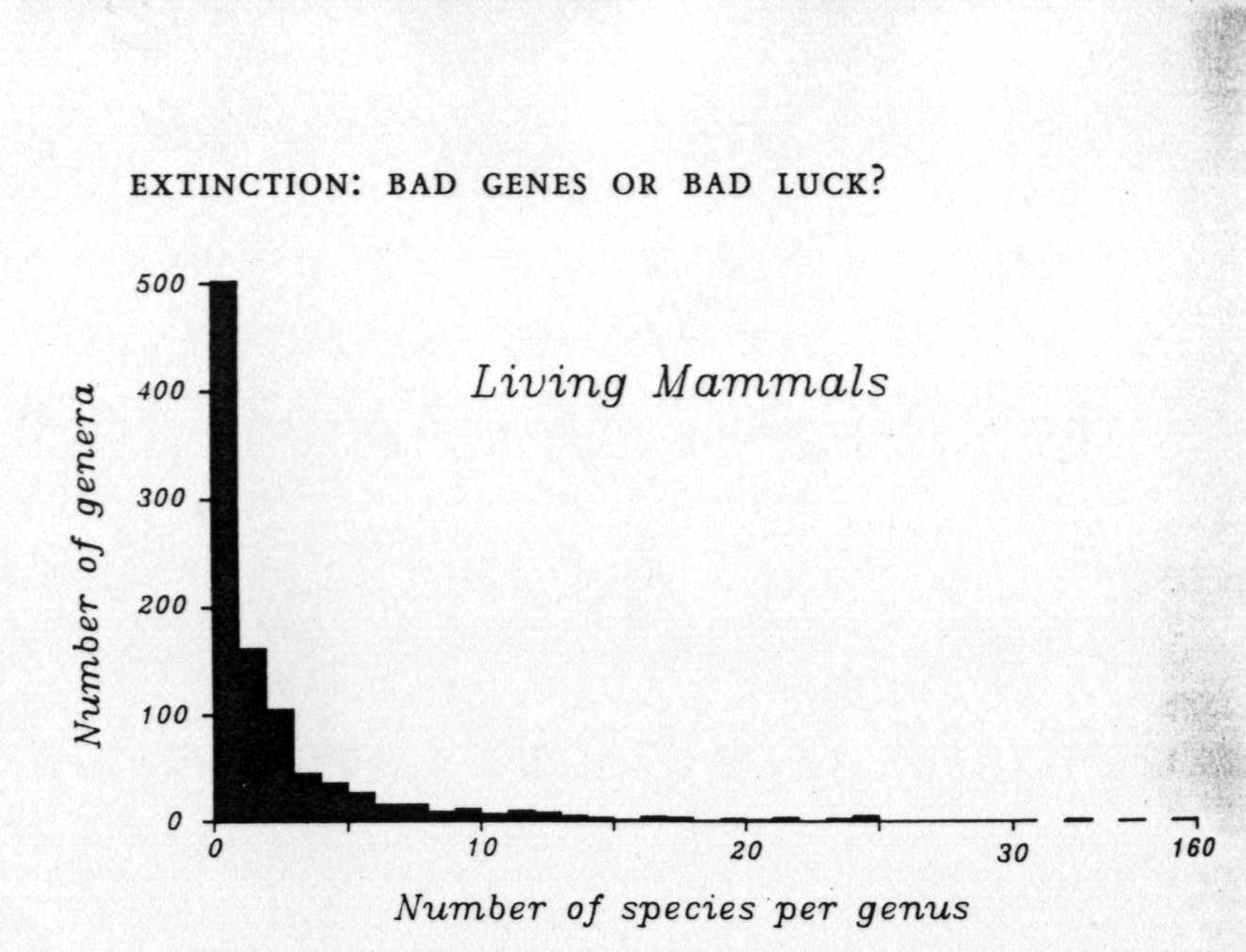
<圖3-3解說:在現生哺乳動物中屬大小的不對稱分佈圖。大約有半數的屬僅有一個種。具有十個種以上的屬非常稀少>
讓我在此對前面所說的一些觀點做些結論。緣於某些理由,從理論及觀察中發展──有些是依據了賭徒破產問題而來──我們得以歸納成下面四點:
(1)大部份的生物種屬都是短命的(比較於其平均值而言)。
(2)大部份的生物種具有很少的個體存在。
(3)大部份的屬具少數的種。
(4)大部份的生物種占有很少的地理區域。
不對稱歪形的變異在自然界中極為普遍。然而奇怪的是,我們大多數人被訓練去相信在自身然現象中變異是呈鐘形分佈,在平均值之上與之下具有相同多的數量──不論我們談到人的身高或體重、氣候、或者籃球賽的分數。沒有事情比這件事更不合事實真象了。
當然,鐘形的曲線(數學中被稱之為常態或者高氏分佈)在自然界中有時確時發生。祇是其它形狀是較為普遍存在的。統計學者牽強於這種問題因為許多最佳的統計學上的測試是設計在鐘形分佈架構之上的。常常他們避開了困境是藉由移轉其原始的資料──換句話說,扭曲了量度的尺度因而他們能夠視其結果好像具有鐘形的分佈。其中之一的類似移轉通常是轉換所有的量度至其對數(有時甚而開平方根上)。假若其移轉的數字具鐘形分佈,分析者就能進一步的測試來假設這種的分佈曲線。
其它的模式
賭徒破產的問題曾經引導我們歸納出關於生物種的事至關緊要於滅絕問題。然而許多模式,尤其是歪形曲線也同時可以約略作用而與賭局或者生物無關。
假設你取一根杖100英尺長,在其間25個隨機的點折斷──不要刻意取中點或任何特定點。結果你得到26個短的杖。現在量度並計算每一個短尺,並做成柱狀分佈圖。其變異形狀會非常像剛剛所提到的生物種屬圖形:一個高峰趨於左方,而在右方有個長長的尾巴延伸而出。圖3-4顯示電腦模擬的結果。
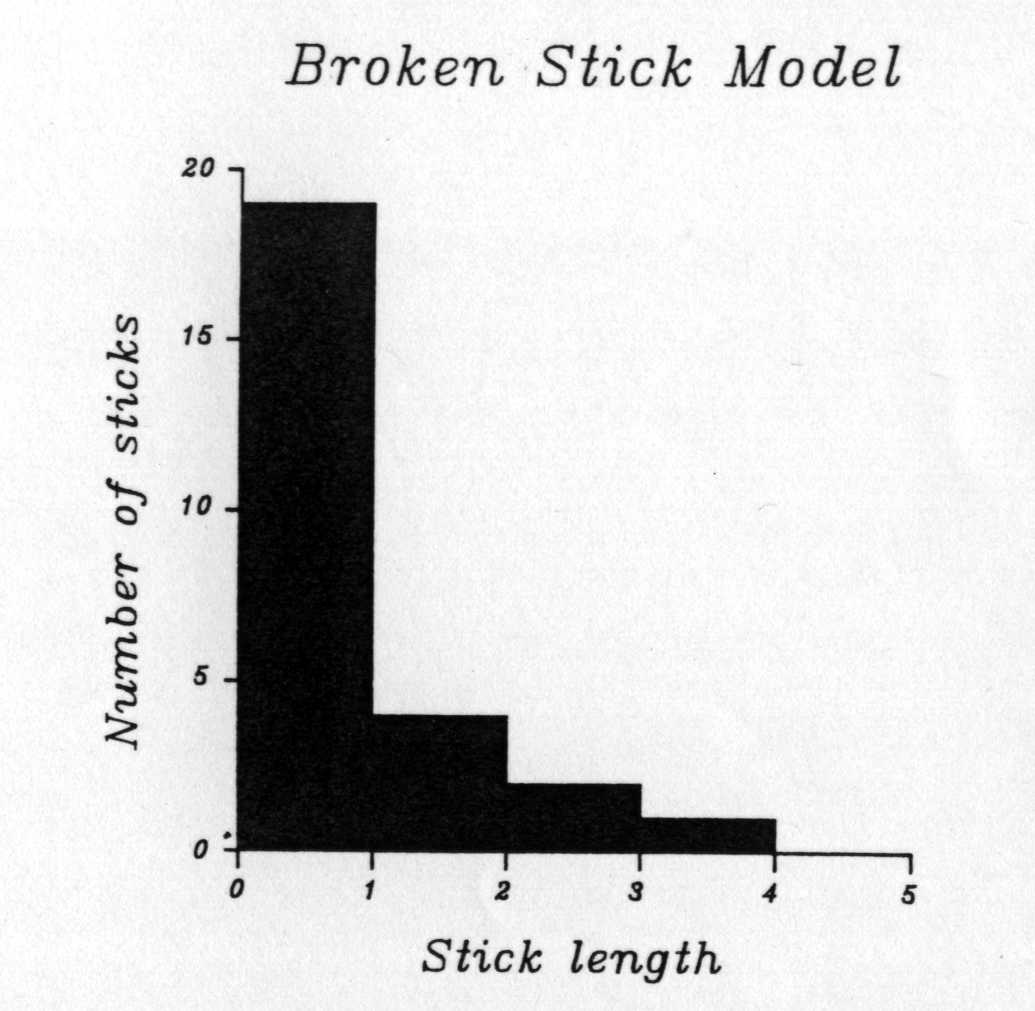
[圖3-4解說:一根長杖在其間隨機選取25個點折斷的電腦模擬圖。這個條形分佈圖顯示了短杖的長短分佈。相當歪斜的情況回想起在自然現象中普遍見到的分佈曲線情況]──折斷長杖的模式
在美國城市人口的大小變異情況也顯示了類似的模式,也像其它許多我們可以量度估算的事項一樣。所謂〝折斷長杖模式〞是許多之一曾經引申到這些模式中,而且許多的研究曾試圖解析尋找出那一種模式最聽來合理或者最合於觀察的結果。為了本書的目的,重要的在於許多分佈曲線是歪曲的形狀。它們和我們所學到的對稱性,鐘形曲線甚而根本不接近。
在滅絕中的一個經驗教訓是從這個分佈曲線中學到,有些植物或者動物,先天上的,比其它的生物要先滅絕。今天存在的絕大部份生物種具有較小的族群並生存在較侷限的地理環境中。這是我們很少注意到的。種族群繁盛且分佈廣泛的最受注意但是在數量上極其稀罕。就是因為這個原因,得以對哺乳動物與昆蟲撰寫控制頁數厚度的有用野外指引書籍。這也就是為什麼,當環變成艱困時,不論是生物性因素或者物理性因素,許多稀有生物種最容易遭致滅絕的厄運。所以,當我們說到某一個滅絕事件消除了40﹪或者80﹪的生物歧異度時,我們也應該特別指出到底是那部份的40﹪或80﹪。這個事件的獨特性將在於這些逝去者是否屬於那些數量繁多,全球分佈的種屬或者僅是局部地區性的特有種屬而已。
家族滅絕的解析
英國18世紀後期/19世紀初期的經濟學家Thomas Malthus被人稱道的是其在人口增長與其社會影響方面的概念研究。其論點認為人口成長永遠是比食物供給要快速,這強烈的影響到達爾文在其發展天擇的理論。因此,非常奇怪的是馬爾薩斯最有名的工作,其人口論專書,應該在滅絕問題的議題上提供一個極重要的扭曲。
在論文中有一小段專注討論在瑞士首府伯恩(Bern)的人口發展情況。馬爾薩斯比較主要家族得姓氏名錄──登錄於中階級的家族成員,例如:商人工匠等等──從一五八三年到一七八三年前後超過兩百年的歷史。明顯的讓馬爾薩斯驚異的在於,在名單最初始的家族有超過四分之三的到最後全然消失不見了。(雖然全體人口的總數是很穩定的)。所有那些消逝的姓氏家族,或者死亡,或者離開伯恩。馬爾薩斯對其觀察結果並沒有解析。而且在這個範例中在作業時並沒有被注意到僅重視於人口的增長而忽略了人口的死亡。
經由了十九世紀,在其它族群中,極高的家族滅絕速率被注意到因為有很好的記錄,尤其是在歐洲皇室家族以及大英帝國的貴族族群中。所有事情是反直覺,反直觀的。每一個人都注意到有許多的家族其姓式能夠追溯回去好幾個世紀。但是統計結果非常堅定。
高程度的姓氏滅絕被大部份觀察者解釋為在上層社會生活時遭受到一些基本上的弱點。資產階層及皇室家族在某種程度上不太可能長命或者生育較多的孩子使其家族持續發展。這種解釋是根據了默企的假設,來自下層社會階層的資料會是顯示較為穩定。有許多年以來,沒有人會去試圖驗証一下。
然而,一個典型的數學研究,在一八七五年由Francis Galton與H.W. Watson發表,顯示了馬爾薩斯原始的觀察確實是期望應該如此的。而當更廣泛的人口普察資料整體人口分佈分析之後,Galton與Watson的結論被証實了。
因此,大部份在人類族群中家族的姓氏具有極令人詫異的短暫生命史。一個新的家族姓氏常常始於一個或非常少的個體,而這個姓氏能否延續幾代,是基於奇特的機運:有多少男孩(姓氏延續的性別)誕生以及他們能否存活再生下後代。任何一個家族的大小波動就像是一個隨機游走型式。假如整體的誕生牽高到足夠造成族群成長,則這種隨機游走或稍為偏向於維繫家族姓氏的存活,但是這種偏頗並不會強到避免賭徒破產的命運,尤其是新的家族開始都是很小的族群。因此,有許多美國人的很大型家族姓氏──像熟知的Smiths及Johnsons是極為少數的。這些家族的成功存活或許類比於哺乳動物中的囓齒類和蝙蝠類的情況。
關於人類姓氏一個最後的說明是在人類族群經過幾千年以來發生了甚麼樣的情況?由於姓氏的滅絕,整個族群必然變成集中於越來越少的幾個家族中,到最終結果(若時間無限延伸)其族群僅剩下一個家族。因為姓氏主要在於分辨或者標示家族的系譜,在任何族群中必然有一些最理想化的數量。當姓氏因為滅絕而變成太少時,我猜想在家族中有強烈的企圖去分支,而新的姓氏開始了。這是一種演化上的分支,但是卻沒有任何在生物世界中可以相提並論的例子。或者有嗎?