夜空中的恆星,有些很明亮,有些就比較昏暗。部分很暗很暗的恆星,還需要用望遠鏡才看得見。在星象模擬軟體的畫面上,會將恆星用大小不等的圓點來呈現恆星看起來的亮度(圖1-36)。看起來比較亮的恆星,就會用比較大的圓點來呈現,這和我們實際上在夜空中看到比較亮的恆星時是一樣的感覺。

早在西元前2世紀,古希臘天文學家喜帕恰斯就將自己觀察到的1000多顆恆星,依照看起來的亮度分成最亮的1等星和最暗的6等星,總共6個等級。到19世紀時,英國天文學家普森將恆星亮度進行精確的量測,他發現喜帕恰斯所定義的1等星和6等星之間,亮度大約相差100倍。於是他沿用舊有的星等,將每一個星等之間的亮度差定義為1001/5(約為2.512)倍,星等相差5等的1等星和6等星之間,亮度差異就是100倍(2.5125=100)。
普森將北極星當成標準的2等星作為比較基準,並量測每一顆恆星的亮度以進行比較,重新將其他恆星的亮度換算成星等,我們稱為視星等。因此,現今對於恆星亮度的描述不再只侷限於1等星到6等星這6個等級,還有比1等星更亮的0等星或-1等星,星等的數值還可以更精確到小數。舉例來說,天狼星的視星等是-1.47,織女星的視星等是0.04。依照星等之間亮度差距的定義,天狼星的亮度是織女星的2.512(0.04-(-1.47))倍(約為4倍)。
由於後來我們發現北極星的亮度會隨著時間有些微變化,所以今天已經不再將北極星當作標準的2等星。
視星等是我們從地球直接觀測恆星看起來的亮度,是我們接收到恆星所輻射出的電磁波能量大小。根據能量會同時往各個方向傳遞的規律,恆星所發射出的能量會隨著傳遞的距離越遠,分散在一個更大的圓球面上(球面的面積和距離平方成正比)。換句話說,如果恆星距離我們越遠,同樣口徑望遠鏡或人類眼睛就只能收到較少的能量(相同面積所接收到的能量越少),恆星看起來的亮度就會越暗,亮度的大小會與距離的平方成反比。於是天文學家定義了一個共同的距離(32.6光年),換算所有距離不盡相同的恆星,在距離地球32.6光年時的亮度,稱之為絕對星等。
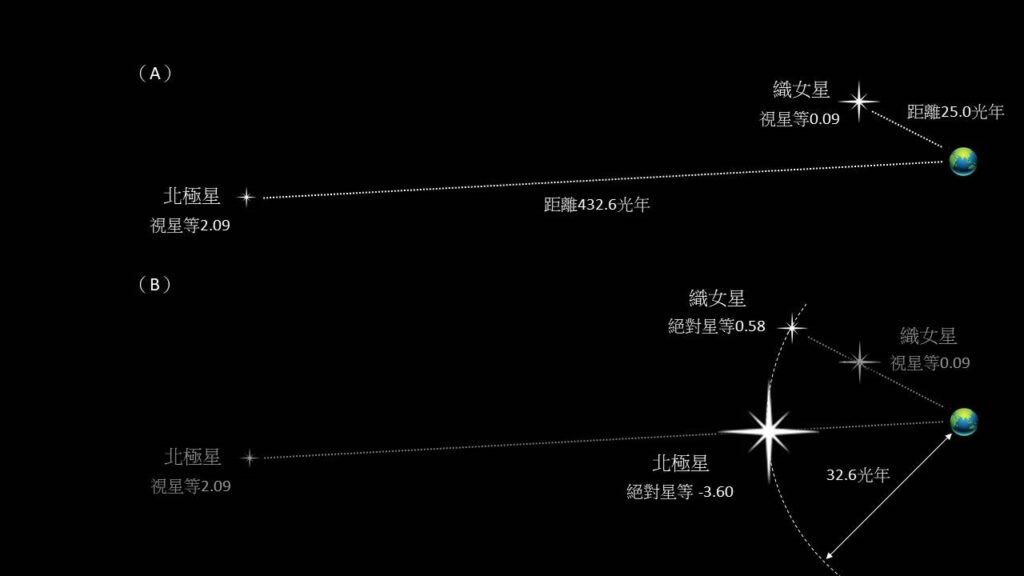
例如織女星的視星等為0.09,距離地球為25.0光年。依照亮度和距離平方成反比的關係,可以計算出來當織女星距離地球32.6光年時,亮度會較暗,絕對星等為0.58。而北極星的視星等為2.09,實際距離地球約432.6光年遠,換算北極星在距離地球32.6光年時的亮度則會亮得多,絕對星等為-3.60(圖1-37)。
我們常會透過觀測近距離恆星的視星等和距離,來推算其絕對星等。再根據這些恆星的其他特徵,像是亮度會週期性變化的變星、或亮度會突然增加到一定程度的Ia型超新星,讓我們可以利用變星的亮度變化週期或Ia型超新星的最大亮度來推論這些恆星的絕對星等。如此一來,對於那些遙遠到無法測量距離的天體,我們就能夠透過這些特徵得知它們的絕對星等,再比較視星等和絕對星等的大小以獲得天體的距離。
由於絕對星等代表每個恆星在相同距離時看起來的亮度,所以也可以說絕對星等就代表恆星的發光能力。一般來說,越高溫的恆星發光能力會較強,看起來會比較亮。除此之外,越高溫的恆星產生的電磁波,還會有不同的能量分布。